Believe it or not, any domestic bond trader under the age of 55 has never traded in a bond bear market. Unlike the stock market, which tends to cycle between bull and bear markets every five to ten years, bond markets can go decades trending in one direction. These long periods of predictable rate movements may seem easy to trade, especially in hindsight, but when the trend changes, muscle memory can trump logic leaving many traders and investors offside.
If you believe higher yields are upon us in the near future, there are many ways to protect your bond portfolio. In this article, we present one idea applicable to municipal bonds. The added benefit of this idea is it does not detract from performance if rates remain stubbornly low or fall even lower. Who says there is no such thing as a free lunch?
Munis
Municipal bonds, aka Munis, are debt obligations issued by state and local government entities. Investors who seek capital preservation and a dependable income stream are the primary holders of munis. In bear markets, munis can offer additional yield over Treasury bonds, still maintain a high credit quality, and avoid the greater volatility present in the corporate bond or equity markets.
Munis are unique in a number of ways but most notably because of their tax status. Please note, munis come in taxable and tax-exempt formats but any reference to munis in this article refers to tax-exempt bonds.
Because of their tax status, evaluating munis involves an extra step to make them comparable to other fixed income assets which are not tax-exempt. When comparing a muni to a Treasury, corporate, mortgage backed security, or any asset for that matter, muni investors must adjust the yield to a taxable equivalent yield. As a simple example, if you are in a 40% tax bracket and evaluating a muni bond yielding 2%, the taxable equivalent yield would be 3.33% (2.00% / (1-40%). It is this yield that should be used to equate it to other fixed income securities.
Negative “Tax” Convexity Matters
Thus far, everything we have mentioned is relatively straight-forward. Less well-understood is the effect of the tax rate on muni bonds with different prices and coupons. Before diving into tax rates, let’s first consider duration. Duration is a measure that provides the price change that would occur for a given change in yield. For instance, a bond with a duration of 3.0 should move approximately 3% in price for every 1% change in yield.
While a very useful measure to help quantify risk and compare bonds with different characteristics, duration changes as yields change. Convexity measures the non-linear change in price for changes in yield. Convexity helps us estimate duration for a given change in yield.
For most fixed rate bonds without options attached, convexity is a minor concern. Convexity in the traditional sense is a complex topic and not of primary importance for this article. If you would like to learn more about traditional convexity, please contact us.
Munis, like most bonds, have a small amount of negative convexity. However, because of their tax status, some muni bonds have, what we call, an additional layer of negative tax convexity. To understand this concept, we must first consider the complete tax implications of owning munis.
The holder of the muni bond receives a stream of coupons and ultimately his or her invested principal back at par ($100). The coupons are tax free, however, if the bond is sold prior to maturity, a taxable capital gain may occur.
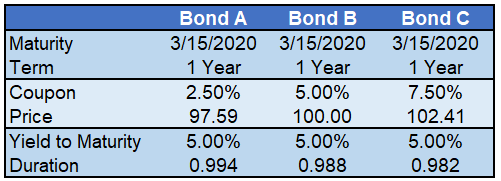
The table below illustrates three hypothetical muni bonds identical in structure and credit quality. We use a term of 1 year to make the math as simple as possible.
In the three sample bonds, note how prices vary based on the range of coupons. Bond A has the lowest coupon but compensates investors with $2.41 ($100-$97.59) of price appreciation at maturity (the bond pays $100 at maturity but is currently priced at $97.59). Conversely, Bond C has a higher coupon, but docks the holder $2.41 in principal at maturity.
For an uninformed investor, choosing between the three bonds is not as easy as it may appear. Because of the discounted price on bond A, the expected price appreciation ($2.41) of Bond A is taxable and subject to the holder’s ordinary income tax rate. The appropriate tax rate is based on a De minimis threshold test discussed in the addendum. Top earners in this tax bracket pay approximately 40%.
Given the tax implication, we recalculate the yield to maturity for Bond A and arrive at a net yield-to-maturity after taxes of 4% (2.50% + (2.50 *(1-.40). Obviously, 4% is well below the 5% yield to maturity offered by bonds B and C, which do not require a tax that Bond A does as they are priced at or above par. Working backwards, an investor choosing between the three bonds should require a price of 95.88 which leaves bond A with an after tax yield to maturity of 5% and on equal footing with bonds B and C.
Implications in a rising yield environment and the role of “tax” convexity
Assume you bought Bond B at par and yields surged 2.50% higher the next day. Using the bond’s stated duration of .988, one would expect Bond B’s price to decline approximately $2.47 (.988 * 2.5%) to $97.53. Based on the prior section, however, we know that is not correct due to the tax implications associated with purchasing a muni at a price below par. Since you purchased the bonds at par, the tax implication doesn’t apply to you, but it will if anyone buys the bond from you after the 2.5% rise in yields. Therefore, the price of a muni bond in the secondary market will be affected not just by the change in rates, but also the associated tax implications. Assuming the ordinary income tax rate, the price of Bond B should fall an additional $1.65 to $95.88. This $1.65 of additional decline in Bond B’s price is the penalty we call negative tax convexity.
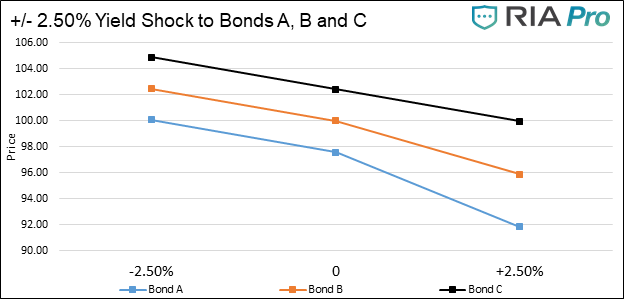
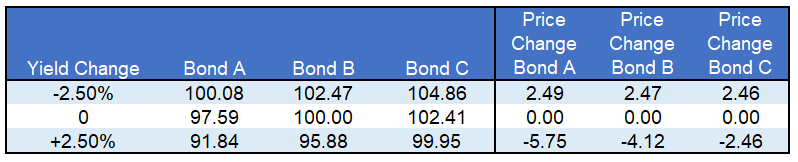
The graph below shows how +/- 2.50% shifts in interest rates affect the prices of bonds A, B, and C. The table below the graph quantifies the change in prices per the shocks. For simplicity’s sake, we assume a constant bond duration in this example.
It is negative tax convexity that should cause investors, all else being equal, to prefer bonds trading at a premium (such as bond C) over those trading at par or a discount. It is also worth noting that the tax convexity plays an additional role in the secondary market for munis. Bonds with prices at or near par will be in less demand than bonds trading well above par if traders anticipate a near term rise in yields that will shift the par bond to a discounted price.
Summary
Yields have fallen for the better part of the last thirty years, so muni investors have not had to deal with discounted bonds and their tax implications often. Because of this, many muni investors are likely unaware of negative tax convexity risk. As we highlighted in the table, the gains in price when yields fall are relatively equal for the three bonds but the negative deviation in price in a rising yield environment is meaningful. Given this negative divergence, we recommend that you favor higher coupon/ higher priced munis. If you currently own lower priced munis, it may be worth swapping them for higher priced (higher coupon) bonds.
Addendum: De minimis
The tax code contains a provision for munis called the de minimis rule. This rule establishes the proper tax rate to apply to capital appreciation. The following clip from Charles Schwab’s Bond Insights provides a good understanding of the rule.
The de minimis rule
The de minimis rule says that for bonds purchased at a discount of less than 0.25% for each full year from the time of purchase to maturity, gains resulting from the discount are taxed as capital gains rather than ordinary income. Larger discounts are taxed at the higher income tax rate.
Imagine you wanted to buy a discount muni that matured in five years at $10,000. The de minimis threshold would be $125 (10,000 x 0.25% x five years), putting the dividing line between the tax rates at $9,875 (the par value of $10,000, minus the de minimis threshold of $125).
For example, if you paid $9,900 for that bond, your $100 price gain would be taxed as a capital gain (at the top federal rate of 23.8%, that would be $23.80). If you received a bigger discount and paid $9,500, your $500 price gain would be taxed as ordinary income (at the top federal rate of 39.6%, that would be $198).
It is important to note that some bonds are issued at prices below par. Such bonds, called original issue discount (OID), use the original offering price and not par as the basis to determine capital gains. If you buy a bond with an OID of $98 at a price of $97.50, you will only be subject to $0.50 (the difference between the OID price and the market price) of capital gains or ordinary income tax.

Michael Lebowitz, CFA is an Investment Analyst and Portfolio Manager for RIA Advisors. specializing in macroeconomic research, valuations, asset allocation, and risk management. RIA Contributing Editor and Research Director. CFA is an Investment Analyst and Portfolio Manager; Co-founder of 720 Global Research.
Follow Michael on Twitter or go to 720global.com for more research and analysis.
Customer Relationship Summary (Form CRS)
Also Read